Análisis del discurso y desarrollo de la noción de número en preescolar y el uso de las TIC

Discourse analysis, development of number sense in preschool education and ICT use

Evelia Reséndiz-Balderas

*Correspondencia: erbalderas@docentes.uat.edu.mx/Fecha de recepción: 11 de julio de 2018/Fecha de aceptación: 26 de noviembre de 2019 Fecha de publicación: 31 de enero de 2020.

Universidad Autónoma de Tamaulipas, Unidad Académica Multidisciplinaria de Educación y Humanidades, Centro Universitario Adolfo López Mateos, edificio de Gestión Del Conocimiento, Ciudad Victoria, Tamaulipas, México, C. P. 87149.

Resumen

Los niños desarrollan habilidades matemáticas en situaciones escolares y no escolares desde edades muy tempranas. El objetivo de esta investigación fue analizar los procesos de enseñanza-aprendizaje en preescolar, donde se encuentra inmersa la noción de número, y por otro lado, el uso de las TIC para el desarrollo de esta noción. La investigación fue de tipo cualitativa y de corte etnográfico, tomando en cuenta el análisis del discurso escolar respecto a la enseñanza de la noción de número. Se tomó como referencia a Piaget y a Vygotsky, debido a que los niños atraviesan diversas y específicas etapas conforme a sus capacidades e intelecto, y los niños aprenden mediante la interacción social. Se identificaron tres principios de enseñanza para favorecer el desarrollo de la noción de número y del conocimiento lógico matemático del niño: la creación de todo tipo de relaciones, la cuantificación de objetos y la interacción social con compañeros y maestras. Con ello, se desarrolla el significado compartido para la noción de número y el uso de la matemática, culturalmente situados en escenarios cotidianos.

PALABRAS CLAVE: educación preescolar, discurso, noción de número.

Abstract

Children develop mathematical skills in school and non-school settings from an early age. The objectives of this study were to analyze: the discourse during teaching-learning processes in which number sense was included and the role of ITC to develop this sense. The research method was a qualitative ethnography where the school discourse employed during the teaching of number sense was analyzed. Piaget and Vygotsky´s constructs were used as a theoretical framework since children undergo diverse and specific development stages according to their skills and intellect, and they similarly learn through social interaction. Three teaching principles were identified that favored logical mathematical thinking and number sense: the creation of all types of relationships, the quantification of objects, and social interaction with classmates and teachers. These principles lead to the development of a shared understanding of number sense and the use of mathematics, culturally situated in everyday settings.

Keywords: preschool education, discourse, number sense.

Introducción

Las matemáticas tienen como objetivo en los primeros años de escolaridad, desarrollar en los alumnos capacidades que les permitirán desenvolverse adecuadamente en situaciones cotidianas. Esta formación inicial puede llegar a condicionar sus oportunidades laborales e ingreso monetario durante la adultez (Fernández y col., 2016; Siegenthaler y col., 2017). Es importante considerar, que dado que el conocimiento matemático se ha constituido y vive socialmente en ámbitos escolares y no escolares (como el mercado, la industria, los laboratorios científicos y muchos otros espacios), su difusión dentro del sistema de enseñanza le obliga a una serie de modificaciones que afectan directamente su estructura y funcionamiento, a la vez que también se afectan las relaciones establecidas entre los estudiantes y el profesor (Reyes-Gasperini y Cantoral, 2019). Es debido a esta necesidad, que el Programa Sectorial de Educación de acuerdo a la Secretaría de Educación Pública (SEP, 2013b), establece como parte de sus prioridades: “Impulsar la educación científica y tecnológica como elemento indispensable para la transformación de México en una sociedad del conocimiento” (p. 15). Para lograr el cumplimiento de dicho objetivo, la SEP (2013a), recomendó en el Plan de Estudios 2011 de Preescolar, la utilización de las tecnologías de la información y la comunicación como una herramienta que contribuya la enseñanza del docente.

Fuenlabrada (2005) mencionó que, uno de los objetivos principales de la SEP, en sus distintos planes de estudio es el desarrollo de la autonomía en los niños sobre su control del aprendizaje. El Programa de Estudios 2011 del nivel Preescolar (SEP, 2013a), se organiza en 6 campos formativos (Tabla 1) que permiten identificar en qué aspectos del desarrollo y del aprendizaje se concentran las actividades escolares en ese periodo.

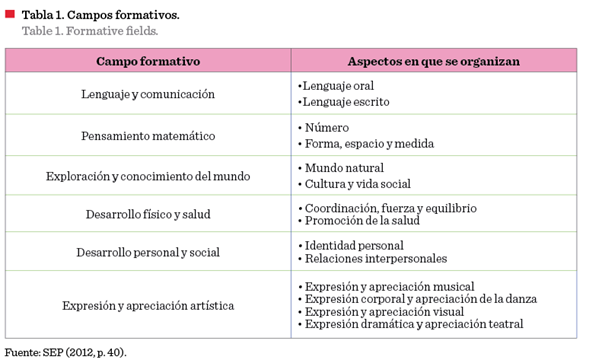
Para esta investigación, se retomó el campo formativo del pensamiento matemático, que se organiza en dos elementos que guardan relación con la construcción de nociones matemáticas elementales: forma, espacio y medida, y el número (SEP, 2013a). Otro apartado importante es el de las competencias, que influyen en los aprendizajes que se desean impartir, es decir, lo que se espera que cada alumno conozca en términos de saber, saber hacer y saber ser. En el campo formativo del pensamiento matemático existen varias competencias, que se indican en la Tabla 2.

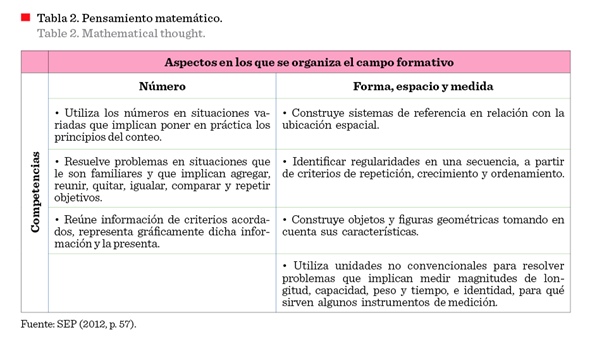
Para los fines de esta investigación se abordó la competencia: “utiliza los números en situaciones variadas que implican poner en práctica los principios del conteo”, perteneciente al apartado de Número. Únicamente se trabajará dicha competencia, ya que el conteo y la utilización de los números son habilidades matemáticas fundamentales para la vida escolar.

Los niños desde edades muy tempranas (3 a 6 años, cuando cursan el nivel preescolar) tienen un acercamiento en su entorno con el número, incluso sin ser conscientes de ello. Vergnaud (2010), afirmó que, durante la educación básica, la noción matemática de mayor importancia para los estudiantes es la noción de número. Cardoso y Cerecedo (2008), mencionaron que la enseñanza de competencias matemáticas en situaciones escolares posee dos atributos principales. El primero, refiriéndose a la habilidad de utilizar los números en situaciones que les permitan la resolución de problemas de su vida diaria. Mientras que, en el segundo, se enfoca en la capacidad de lograr el entendimiento y la interpretación de conocimientos matemáticos más abstractos y de mayor complejidad. Para Cantoral (2019), el problema educativo no es de la constitución de objetos abstractos, sino el de su significación compartida para el uso culturalmente situado. Por tanto, su objetivo no estará en modificar, reorganizar o reestructurar la enseñanza de conceptos y procedimientos algorítmicos de las matemáticas, con el objetivo de lograr el aprendizaje, sino, en poner en juego un conjunto de prácticas socialmente compartidas en el mundo de experiencias del aprendiz, dentro y fuera del aula, y a lo largo de todas las actividades de su vida diaria.

Los niños, al contar objetos suelen saltarse unos y seguir contando otros. Esto demuestra que, ellos no sienten la necesidad lógica de ordenar los objetos de una manera estructurada para validar que su proceso es correcto. Los niños, al ingresar al preescolar, presentan dificultades para realizar operaciones de razonamiento. Según Kamii (2003) al mostrarles un número escrito y tener el mismo número de figuras a un lado, ellos sí los relacionan, pero si las figuras son invertidas, cuando su forma cambia o el contexto se altera, la enseñanza puede verse afectada.

Para este trabajo, se utilizaron dos teorías para el análisis de las situaciones de clase. La primera, es la teoría de Piaget (1973), que menciona que los niños atraviesan por distintas etapas conforme a su madurez cognitiva y capacidades, para percibir las relaciones. La segunda teoría sostiene que los niños aprenden mediante la interacción social (Vygotsky, 2000). La interacción con otros contribuye para que los niños sean capaces de apropiarse de formas de pensar y de convivir de una determinada sociedad. Estas teorías ayudan a comprender los procesos cognitivos en los que se encuentran los alumnos del nivel preescolar, también, para entender e interpretar el rol que juega la socialización de los estudiantes con los demás actores educativos y con el contexto que los rodea.

De acuerdo con Vygotsky (1984): “Todas las funciones psicointelectivas superiores aparecen dos veces en el curso del desarrollo del niño”; primero, en la sociedad (actividades interpsíquicas); y después, en el plano individual (funciones intrapsíquicas). Señala el autor que, un ejemplo de ello es el lenguaje, que surge “como medio de comunicación entre el niño y las personas que lo rodean”, y luego se transforma en un lenguaje interno, es decir, el pensamiento interno del niño. Vygotsky añadió que, “estas interrelaciones son también el origen de los procesos volitivos del niño”, por ejemplo, el sentido moral, que de acuerdo con Piaget, es favorecido por la cooperación.

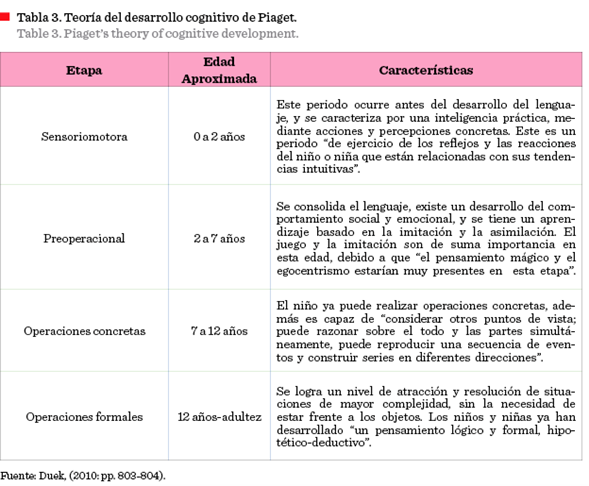
Duek (2010) hace un análisis de la Teoría del Desarrollo Cognitivo postulada por Piaget. Dicha teoría está conformada por cuatro etapas (Tabla 3), definidas por un periodo aproximado de tiempo, y con características específicas de desarrollo cognitivo. Para esta investigación, la etapapreoperacional tiene especial importancia, debido a que los estudiantes del nivel preescolar se encuentran precisamente en esta etapa.

Por otro lado, las computadoras se han convertido en una herramienta útil para el proceso de enseñanza-aprendizaje de las matemáticas, jugando también un rol cultural esencial para la sociedad actual. Investigaciones como las realizadas por Pérez (2014) y Lezcano y col. (2017) validan estas afirmaciones, debido a que comprobaron que la utilización orientada de softwares especializados contribuye significativamente para las clases de matemáticas en todos los niveles educativos, ya que los estudiantes presentaron una mayor motivación, dinamismo y rendimiento en clase. La utilización de software educativo puede ser beneficioso para estudiantes y docentes en la construcción de conocimiento. Por eso, en los últimos años, ha surgido un conjunto de investigaciones cuyo propósito es comprobar las bondades y debilidades de la implementación de las tecnologías en las matemáticas (Fernández y col., 2017).

El objetivo de esta investigación fue analizar, por un lado, los procesos de enseñanza-aprendizaje en preescolar, en los que se encuentra inmersa la noción de número, y por otro lado, el uso de un software para reafirmar lo visto en clase.

MATERIALES Y MÉTODOS

El estudio se llevó a cabo en un Centro de Desarrollo Infantil (Cendi), ubicado en una zona urbana en Ciudad Victoria, Tamaulipas, México. La muestra fue de 23 alumnos, de los cuales, 9 eran niñas y 14 niños. Todos pertenecían al grupo de preescolar 3º “A” y sus edades oscilaban de los 5 a 6 años. Se seleccionaron estos participantes debido a que en este grado los niños estudian la noción de número, y se inician en la competencia que la incluye (utilizan los números en situaciones variadas que implican poner en práctica los principios de conteo).

La investigación fue de tipo cualitativa, de corte etnográfico y toma como referente el análisis del discurso escolar. La etnografía aplicada en educación tiene el objetivo de comprender los significados y sentidos que se encuentran presentes para los actores educativos de las situaciones escolares. Esta metodología se encuentra dentro de las líneas de investigación cualitativas. En general, tiene la finalidad de concentrarse en el conjunto de hechos que se llevan a cabo durante las prácticas educativas entre docentes y alumnos.

El discurso como comunicación se origina y desarrolla en estrecha relación con el estudio de la interacción didáctica, en la relación docente-alumno-contenido. Esta perspectiva se apoya en la noción de comunicación y en la consideración de que la función primordial del lenguaje es la comunicación humana. Es decir, el lenguaje se concibe como un vehículo de comunicación. Es debido a lo anterior, que el análisis del discurso matemático escolar es de suma importancia para el entendimiento de la realidad escolar. Sierpinska (1994), estableció una diferencia entre las explicaciones científicas y las didácticas. Las científicas, cuyo objetivo es llegar a unas bases conceptuales del entendimiento; y las didácticas, que se dirigen a unas bases familiares del entendimiento (una imagen o sólo algún conocimiento previo y experiencias), frecuentemente son llamadas así en el ámbito de la enseñanza. Estas se tomarán en cuenta para el estudio. Otra investigación enfocada en la interacción verbal en el aula es la realizada por Bartolini (1998), con un experimento de enseñanza de coordinación de perspectivas espaciales, y discute una metodología de análisis para las transcripciones.

En este trabajo, se consideraron 6 etapas, empleando una metodología similar a la utilizada por Reséndiz (2004): recopilación de datos, elaboración de registros de la observación, el análisis y discusión de los resultados obtenidos, síntesis e interpretación global, integración de los productos de la investigación, y la redacción del informe correspondiente.

Dentro del salón de clases, se observaron y grabaron las sesiones donde se trabajó con la noción de número, las estrategias y materiales que se utilizan para las explicaciones; cuando la maestra lo consideraba pertinente, trasladaba a los niños a un centro de cómputo (2 niños por computadora), donde a través del software Gateando con el ratón, realizaban algunas actividades de conteo. Para encontrar la respuesta correcta lo hacían a través del ensayo y error.

En los estudios cualitativos, a diferencia de los cuantitativos, el análisis de datos no tiene vías de salida muy definidas, como la aplicación de un método o de algoritmos de procesamiento a los datos recopilados. Una de las dificultades radica, precisamente, en la determinación de un método. En este apartado se presentan las categorías de análisis con las que se elaboraron interpretaciones y estudios en direcciones específicas. De los momentos abordados, se decidió atender a las situaciones que se repiten y que permiten inferir algunas reglas de la interacción en el aula, así como recoger y analizar otras de excepción, como también se señala en Candela (1999).

Las categorías de análisis se construyeron mediante la conceptualización del fenómeno y la categorización de su análisis, mediante el acercamiento directo con el espacio escolar (Reséndiz, 2004). Se buscó que coincidieran con los objetivos, campos formativos, y competencias planteados, tanto en los planes y programas de estudio, como en los objetivos del software Gateando con el ratón.

El programa lúdico-didáctico Gateando con el ratón, recopila materiales didácticos multimedia para el desarrollo de las habilidades matemáticas en la educación preescolar. Este programa fue creado por Rodríguez y Norato (2004), en conjunto con el Centro Estatal de Tecnología Educativa de la Secretaría de Educación de Tamaulipas, quienes intervinieron con bases firmes en el desarrollo de ideas y la conformación de los contenidos digitales del proyecto educativo. En el programa Gateando con el ratón se trabaja mediante módulos. En total hay siete módulos que contienen actividades, para que los alumnos puedan aprender mediante el juego (ensayo y error), y estas actividades (Tabla 4) contienen acciones de conteo.

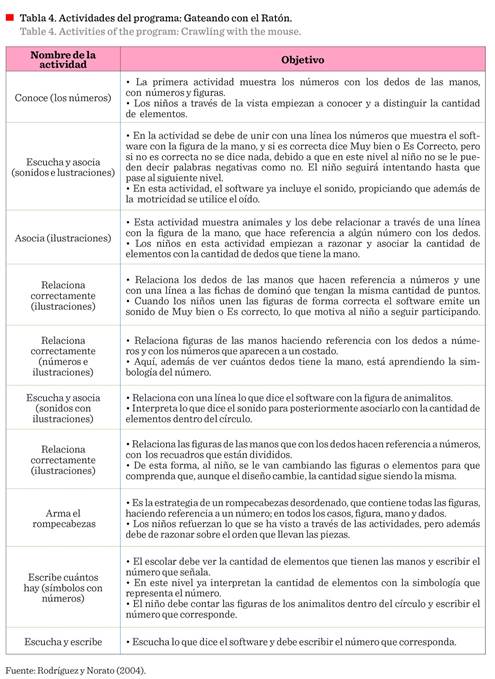
De acuerdo con Hernández y col. (2014: 7-8), la revisión de la literatura “puede complementarse en cualquier etapa del estudio y apoyar desde el planteamiento del problema hasta la elaboración del reporte de resultados […] En la investigación cualitativa a veces es necesario regresar a etapas previas”. Por ello, las categorías de análisis pueden surgir de los datos mismos (transcripciones), pero también de la revisión teórica. Se complementaron mediante una aproximación inicial a los datos recolectados.

Las categorías de análisis son:

-El número, valor y la forma de las monedas

-El número, su significado y signo.

-La asociación de los números y la cantidad de billetes

-El valor de las monedas.

Análisis de las estrategias

En este apartado se analizan las estrategias usadas en el aula seleccionada para el estudio, así como el software empleado en el logro de la competencia.

RESULTADOS Y DISCUSIÓN

El número, valor y la forma de las monedas (la creación de todo tipo de relaciones y la interacción social).

En la sesión de clase, se pudo ver que la maestra fomentó activamente la participación y que los alumnos relacionaron los números mediante las monedas. También se observó que la maestra, al frente de los niños, reafirmó en el pintarrón lo mencionado por los alumnos; repitió lo que ellos dijeron, para reforzar el contenido de la clase. Se transcribe, a continuación, el extracto de una sesión de clase:

Maestra (M): A ver, existen monedas, ¿de qué cantidad?

Alumno (Ao 5): De un peso

M: De un peso.

Ao 4: De dos pesos.

M: (Las dibuja en el pintarrón.) La de dos pesos es un poco más grande; existen monedas de dos pesos […] ¿Hay monedas de tres pesos?

Todos (T): Sí, no.

M: No […] Hay una moneda, ¿de cuánto?

T: De cuatro. De cinco.

M: De cinco.

Ao 4: (Se levanta y le pide el plumón a la maestra; dibuja en el pintarrón). Es una pequeña, así, mira, muy pequeña, que tiene el número diez.

M: Ah, hay una moneda muy pequeñita (hace la forma con la mano), que tiene el nú-mero diez, pero ahí no son diez pesos, son diez centavos.

¿Existen monedas de cinco pesos? ¿Quién quiere pasar?

T: (Se ponen de pie, levantan la mano). Yo.

Yo.

M: (Los tranquiliza). En orden, en orden. Tú ya pasaste, siéntate allá […] (Ao 6, pasa al pintarrón a dibujar el número 5).

Los fragmentos presentados en este trabajo son tomados de Reséndiz y col. (2014).

La maestra pregunta de qué cantidad existen monedas, para que ellos respondan (es importante señalar que la investigación se realizó en México, la moneda empleada fue el peso mexicano); uno contesta que de un peso, a lo cual la maestra responde con las mismas palabras para reforzar el conocimiento; posteriormente, otro niño afirma de dos pesos y entonces la maestra dibuja las monedas que corresponden a cada número, logrando que mediante su dibujo se destaque el número y la forma. La maestra comienza la secuencia, haciendo una evaluación inicial, preguntando a los alumnos por el tipo de monedas que conocen. La maestra adquiere un papel muy importante, porque es la mediadora entre el contexto en el que se desenvuelven los niños, las herramientas y los estímulos en beneficio del desarrollo de ellos. En la interacción social, se pone en juego un conjunto de prácticas socialmente compartidas (noción de número) en el mundo de experiencias del niño dentro y fuera del aula. Sfard (2002) mencionó que el discurso a enseñar se desarrolla con base en los discursos de los niños, que ya poseen conocimiento: el maestro nunca parte de cero. Es por eso que propone un método comunicacional para la cognición, en el que se estudia un sistema que permite estar en sintonía con las interacciones donde se origina el cambio. La interacción social con compañeros y maestra anima a los niños a intercambiar ideas. Vygotsky (2000) sostenía que lo que los niños pueden hacer en las interacciones sociales, con el tiempo, pasa a formar parte de sus repertorios independientes.

Después, los niños quieren dibujar en el pintarrón alguna de las monedas, la maestra accede, siempre buscando que todos participen y es aquí cuando surge una nueva interrogante: al hacer 2 monedas que tienen el mismo número, la maestra les señala con sus manos y haciendo la forma manifiesta que sí hay otra moneda de diez, pero que es más pequeña y que se trata de centavos.

Los niños van mencionando cómo son las monedas, las relacionan con su tamaño y destacan que, aunque algunas de las monedas tienen el mismo número, su cantidad es diferente. En esta parte se refuerza el tema de los números y las formas, pasando a los infantes al pintarrón, para que dibujen las monedas y le pongan la cifra que les corresponde, de acuerdo con el tamaño que tienen. De este modo, se le enseña al niño la forma que tienen las monedas y el número.

Piaget (1973) señaló que los infantes, mediante la utilización de palabras e imágenes mentales, aprenden a relacionarse de una manera mucho más compleja con su ambiente. Esto quiere decir que los niños relacionaron las formas y el valor porque ya los conocían; tal vez por ir a la tienda o escuchar hablar del dinero en su vida diaria, entre otras situaciones. Así se logra que el niño relacione las imágenes que tenía en su mente con el tema visto en el aula. La creación de todo tipo de relaciones, anima al niño a estar atento y a establecer todo tipo de relaciones entre toda clase de objetos, acontecimientos y acciones. El niño construye el número a partir de todos los tipos de relaciones que crea entre los objetos. La construcción social del conocimiento, se constituye mediante procesos deliberados para el uso compartido de conocimiento. Se trata de mecanismos constructivos y de carácter social, que producen interacciones, explícitas o implícitas, entre mente, conocimiento y cultura (Cantoral y col., 2014).

El número, su significado y signo (la cuantificación de objetos y la interacción social)

La participación, al igual que la clase, es guiada por la maestra. Los niños, después de conocer las formas en las que se usa el dinero, deben identificar el signo de pesos que lo representa, ($) en este caso, para que lo asocien a los números y definan, entonces, que van a trabajar con una representación del dinero. Los niños aprenden que el símbolo de pesos es el que le da valor al número. Ellos mismos comentaron que sólo debe leerse o decirse el número, sino que también es bueno mencionar el valor que representa. Así se interpreta en el siguiente extracto:

M: (Se vuelve y escribe en el pintarrón). Rectángulo: los billetes reales son en rectángulo […] ¿qué tiene este billete?

Ao 2: (Levanta la mano para participar). Una “s” y un palito.

M: (Escribe en el pintarrón y deletrea para los niños). Una “s” y un palito; y ¿eso qué significa?

Ao 7: El signo.

M: El signo, ¿de qué?

Ao 8: De número, para que no nada más diga peso o uno. […]

M: ¿La moneda también tendrá el signo de pesos?

T: No.

M: Sí, sí, porque estamos hablando de […] pesos.

Ao 6: Signos.

M: De pesos.

[…]

M: Ahora vamos a ver los billetes. Los billetes tienen forma de una figura geométrica que

es un […]

T: Rectángulo.

M: Rectángulo.

Ao 4: Ése se parece a un robot con ojos de dinero.

M: (Está dibujando en el pintarrón). Mmm […] le ponemos el signo de pesos porque vamos a manejar pesos […] ¿Quién conoce los billetes?

La maestra empieza a dibujar rectángulos en el pintarrón para preguntarles a los niños cómo son los billetes reales, a lo cual uno de ellos responde describiendo el signo y, entonces, otro de sus compañeros señala que a ese símbolo se le denomina signo de pesos y sirve para que un número adquiera un valor.

Se cuestiona a los alumnos si las monedas tendrán este signo y todo el grupo responde que no; entonces la maestra los corrige diciéndoles que también las monedas lo tienen, debido a que tienen un valor y por eso deben tener el signo de pesos. En esta actividad la maestra buscó desarrollar el aprendizaje esperado, porque “utiliza objetos, símbolos propios y números para representar cantidades, con diferentes propósitos y en diversas situaciones”.

En la anterior transcripción se aprecia que algunos de los estudiantes comentan sus experiencias personales y aprendizajes previos. Es en este sentido, que se debe retomar la afirmación de Vygotsky (2000: 192), respecto de la relación desarrollo/aprendizaje: “el aprendizaje del niño comienza mucho antes del aprendizaje escolar. El aprendizaje escolar jamás parte de cero. Todo aprendizaje del niño tiene una prehistoria. Bartolini (1998) añade que el nuevo conocimiento matemático (individual o compartido) que se construye en el aula se da por medio de las interacciones y conversaciones entre profesores y alumnos. Dicho autora menciona que el doble movimiento, entre el sentido personal de un concepto y el significado matemático compartido, resulta crucial para que el aprendizaje se lleve a cabo; el papel del maestro y los estudiantes determina su surgimiento. La interacción social con compañeros y maestra anima a los niños a intercambiar ideas.

En este apartado, los alumnos identifican que los billetes, las monedas y su número adquieren un valor cuando están acompañados del signo de pesos. Esto comprueba lo dicho por Piaget (1973), que los niños empiezan a entender palabras más complejas en su periodo preoperatorio; esto resalta cuando ellos entienden cómo es y para qué sirve el dinero. La cuantificación de objetos anima al niño a pensar sobre los números y las cantidades de objetos, cuando tienen significado para él.

La asociación de los números y la cantidad de billetes (la creación de todo tipo de relaciones y la interacción social)

La maestra dibujaba en el pintarrón tres rectángulos, poniéndoles el signo de pesos, esto para que los alumnos pudieran identificar la cantidad de billetes manejados, posteriormente sentaba a los alumnos en el piso, en forma de media luna, para preguntarles cuáles eran los números que tenían los billetes.

A continuación, se mostrará un extracto de clase en donde los alumnos comienzan a relacionar los números para tener cantidades mayores a 2 cifras:

M: Hay billetes, ¿de qué cantidad? (Detiene la clase para tranquilizar a los alumnos).

Ao 3: De un peso.

Ao 4: De mil pesos.

M: (Manda sentar a los niños que andan de pie).

¡Siéntate, siéntate!

Ao 5: De ochocientos pesos.

M: Hay billetes de veinte pesos. ¿Quién sabe escribir el número veinte?

T: Yo. Yo.

M: (Pasa al pintarrón). A ver, Alumna 1 (Aa 1); vamos a dejar a Aa 1. En el de arriba, escribe el número veinte.

Ao 3: Maestra ya sé dónde está la cámara.

M: Ya, guarda silencio.

Ao 4: No alcanza, no alcanza.

M: Bueno en el de abajo; ahí: veinte pesos.

Ao 5: Un veinte, un dos y uno […]

M: Muy bien. Hay otro billete que es de cincuenta pesos, ¿cómo se escribe el cincuenta?

T: (Levantando la mano para participar). ¡Yo!

¡Yo!

M: A ver, ¿cómo se escribe? […] a ver Aa 2, Aa 2 no ha pasado. ¿Cómo se escribe el cincuenta?

Aa 2: cinco y cero.

M: Un cinco y un cero, muy bien; en el de arriba, a ver si alcanzas. Un cinco y un cero, muy bien. Hay otro billete de cien pesos.

T: (Hablan a la vez, intentan pararse y levantan la mano). ¡Yo! ¡Yo!

M: No, no, a ver: primero me tienen que decir cómo se escribe el cien. Desde su lugar.

Ao 4: Un uno y un cero, y un cero.

La maestra les pregunta a los alumnos si quieren participar, y permite que de uno en uno pasen al pintarrón a escribir las cantidades a los billetes, con la condición de que antes de pasar, digan cómo se forman. Para que los alumnos entren en confianza, la maestra se sienta en el piso con ellos. La creación de todo tipo de relaciones animan al niño a estar atento y a establecer todo tipo de relaciones entre toda clase de objetos, acontecimientos y acciones. La interacción social con compañeros y maestra, anima al niño a intercambiar ideas con sus compañeros. En este sentido, Cantoral (2016) dice que la sociopistemología considera a las prácticas sociales como la base del conocimiento, en la medida en que son el sustento y la orientación para llevar a cabo una construcción social del conocimiento matemático. Al contextualizar las problemáticas, los educandos tendrán herramientas para poder dar significado a los procedimientos que tienen que seguir. Con la estrategia, la prioridad es rescatar los conocimientos matemáticos del estudiante, identificando sus usos en escenarios de lo cotidiano, donde se rescate el conocimiento de la gente, del que aprende. En este sentido, para Vygotsky (2000) los escenarios sociales crean zonas de desarrollo próximo, que al principio operan no sólo en las interacciones cooperativas, pero, gradualmente, los procesos suscitados se internalizan, se convierten en parte del logro evolutivo independiente del niño.

Una vez que la maestra concluyó la actividad que llevaba por nombre “La tiendita”, acudió con los alumnos al centro de cómputo para realizar actividades que puedan reforzar el ejercicio anterior.

Centro de cómputo

Se trabajan las actividades con el software, los primeros números por vía visual directa, además de escuchar y asociar los sonidos con los dedos, asociar el número de dedos con el número de figuras, relacionar figuras con los dedos, relacionar correctamente números y dedos, asociar la figura con el sonido, armar rompecabezas, imagen para escribir cuántos dedos hay, imagen para escribir cuántos objetos hay (Tabla 4), donde se busca que asocien imágenes de cada número con los instrumentos más usados en la escuela: los dedos de las manos, las regletas y los puntos de los dados.

Esta transcripción, corresponde al arribo de los alumnos al centro de cómputo para iniciar la clase con la maestra:

MC: Van a tomar la actividad de arriba, que dice (1 al 4), y ahí comienzan a trabajar.

Ao 1: ¿Aquí, maestra, aquí?

MC: Sí, ahí. Si tienen alguna duda, levantan su mano para preguntar; acuérdense que los deditos, el dibujo que viene ahí, nos va indicando la cantidad.

Los estudiantes comienzan la manipulación del software usando la estrategia de ensayo y error, esto permite intentarlo las veces que sean necesarias hasta que encuentren con la respuesta correcta, lo ven como un juego. La primera actividad muestra los números con los dedos de las manos, con números y figuras. Los niños a través de la vista empiezan a conocer y a distinguir la cantidad de elementos. Una vez que se obtiene la respuesta se prosigue al siguiente nivel. Con el pasar de las actividades, la mayoría de los niños se fueron familiarizando con el software. Cuando los estudiantes presentaban dificultades para la comprensión de las actividades, eran auxiliados inmediatamente por la maestra del salón de cómputo, para la resolución de sus dudas. Así eran las sesiones en el centro de cómputo, se dejaba a los niños que jugaran contestando mediante ensayo y error, de relacionar, escuchar, escribir, relacionar, asociar, etc.

La maestra colocaba a dos niños por computadora para que se apoyaran. Al respecto, Vygotsky (2000) mencionó que cuando los estudiantes trabajan en equipo, tienen la oportunidad de enriquecer sus aprendizajes por medio del trabajo colaborativo.

Los niños en las sesiones en el centro de cómputo, usan estrategias de conteo, también relacionan formas geométricas con los dedos de las manos, asocian la figura y la motricidad. De la competencia “utiliza los números en situaciones variadas que implican poner en práctica los principios de conteo”, se puede decir que en el centro de cómputo están poniendo en práctica el conteo a través a través de las diferentes actividades. La noción de número se va mostrando a través de diferentes formas, como es la relación, asociación, identificación y correspondencia, conforme van recorriendo las actividades. Es evidente que, en este trabajo, la observación de estos procesos no tuvo el tiempo necesario, para adentrarse en la manera en que cada alumno se aproxima al aprendizaje, pero es relevante considerarla, porque en el futuro será incluida en otra investigación.

El valor de las monedas (la cuantificación de objetos)

Para esta parte de la actividad, la maestra titular pega una cartulina al frente y se sienta en el piso con los niños. Empieza preguntando cómo son las monedas y ellos responden; posteriormente, pasan a la cartulina y dibujan la moneda con el signo de pesos y los números que le corresponden.

Para definir aún más el número, la maestra forma equipos y les pone la actividad de realizar las monedas con hojas de cartulina y plumones. Al hacer el trabajo en equipo, los estudiantes tienen la posibilidad de apoyarse, corregirse y cuestionarse. Vygotsky (1984) argumentó que las actividades compartidas ayudan a los niños a interiorizar las formas de pensamiento y conducta de su sociedad, a apropiarse de ellas. La mediación pedagógica adquiere un papel muy importante, ya que habrá de considerar el contexto en el que se desenvuelven los niños, sus características, necesidades de aprendizaje, los propósitos que plantea el programa de estudios, así como las competencias y/o saberes que pretende desarrollar (Reyes y Garza, 2019).

M: Y, a ver: ¿todas las monedas son del mismo tamaño?

T: Maestra, no.

M: ¿Qué figura geométrica tiene la moneda?

T: Pequeñita, chiquita.

M: Pero ¿qué figura geométrica?

Ao 4: (En el aire, traza un círculo con su ma-

no). Circular.

M: Ah, muy bien; bueno, aquí tengo la moneda. Miren: son de diferente tamaño; la más pequeña, ¿cuánto vale?

T: Uno.

M: Uno. Después, ¿sigue […]?

T: Dos, tres. M: Tres, ¿hay alguna moneda de tres?

T: No.

M: ¿De qué sigue?

Ao 5: Cinco.

M: ¿Y por último […]?

T: Cinco, diez.

M: (Invita a los niños a participar en la dinámica de dibujar el número de las monedas

en el pintarrón). ¿A ver, Ao 9 qué valor tiene esa moneda?

Ao 9: De un peso.

M: De un peso; ahora, vamos a ver la moneda que vale dos pesos. A ver Aa 3, pásale a escri-

bir el número dos en la moneda de dos pesos. ¿Cuál crees tú que sea la de dos? (Aa 3 señala la moneda donde va a escribir el dos). Muy bien, muy bien. ¿Quién me ayuda con la moneda de cinco pesos?

T: ¡Yo! ¡Yo!

M: A ver, Aa 4, pasamos a Aa 4 (Pasa al pintarrón); ayúdame con la moneda de cinco pesos

[…] ¿Está correcto ese número?

T: No, no.

M: Hay que modificarlo (Los alumnos intentan corregir).

Ao 1: Yo ya sé.

M: A ver, Ao 1, ahí, a un ladito, volvemos a escribir; está bien, Aa 4, nada más que lo hici-

mos al revés. El cinco otra vez. No (Señala a otra moneda más grande). No, en la otra, donde escribió Aa 4, abajo.

Ao 6: (Se acerca a ayudar a su compañero). Mira, aquí Ao 1.

M: Ahí, ándale, ahí; vamos a escribir el valor número cinco.

Ao 6: (Señala y apoya a su compañero). Como este, pero al revés.

M: Ahorita le vamos a tapar el número que está al revés. A ver, quien esté en su lugar es

el que me va a ayudar con el valor de la moneda de diez. A ver Aa 5, pásale Aa 5: la moneda más grande, ¿cuánto vale?

T: Diez.

M: Diez pesos; vamos a escribir el número diez, muy bien, Aa 5. La moneda más grande vale diez pesos. A ver, Ao 9, ¿qué billetes hicimos el día de ayer? Ao 1: nos sentamos en nuestro lugar.

En esta actividad, la maestra empieza por describir los diferentes tamaños y formas que tienen las monedas, dejando en claro que las más pequeñas tienen menor valor. Se muestra uno de los aprendizajes: “identifica el orden de los números en forma escrita, en situaciones escolares y familiares”. La profesora refuerza los contenidos que habían adquirido anteriormente haciendo un recorrido por las diversas monedas que existen, logrando que los niños participen en el diseño y su número, para lograr la correspondencia y el valor que tiene cada una con su respectiva cifra.

Otro punto importante es que la actividad, en todo momento fue guiada por la maestra, aunque también les daba cierta libertad, estuvo presente en todo el proceso de aprendizaje. Vygotsky (1984) mencionó que durante el proceso de aprendizaje, los adultos siempre deben dirigir el aprendizaje de los niños, para que este pueda dominar o interiorizar dicho conocimiento. La importancia de que actúen otras personas en el desarrollo del niño se torna particularmente evidente en aquellas situaciones en las que el aprendizaje es un resultado claramente deseable de las interacciones sociales. En la escuela, por lo tanto, donde el aprendizaje es el objetivo de un proceso que se propone guiar hacia un determinado tipo de desarrollo, se privilegia la intervención deliberada. La intervención del profesor desempeña, pues, un papel central en la trayectoria de los individuos que pasan por la escuela.

La supervisión de la maestra y la interacción entre estudiantes que fueron observadas en este trabajo, son elementos fundamentales en la construcción y desarrollo de la noción de número. La mediación del docente adquiere un papel muy importante, ya que considera el contexto en el que se desenvuelven los niños, sus necesidades de aprendizaje y los propósitos que plantea el plan de estudios de preescolar, así como las competencias y saberes que pretende desarrollar.

Fuenlabrada (2009) y Hernández y Pérez (2018) coinciden en que las educadoras deben propiciar la confrontación con problemas, debido a que esto es fundamental para el desarrollo de nociones matemáticas. Resolver problemas en situaciones que les son familiares y que implican agregar, reunir, quitar, igualar, comparar y repetir, son algunos de los procesos de enseñanza y aprendizaje identificados, que contribuyen al desarrollo de la noción de número. En este tipo de actividades se permite que los estudiantes formen sus propias conjeturas racionales, mediante la utilización de contenidos que pueden emplear en situaciones de su contexto inmediato (Cardoso y Cerecedo, 2008).

Cabe destacar que las sesiones del aula van más allá de sólo enseñar la utilización de los números; es una actividad más compleja, ya que permite que los infantes sean más críticos porque, además de conocer la representación del dinero, interpretan que el número no tiene valor monetario sin el signo de pesos. La cuantificación de objetos, anima al niño a pensar sobre los números y las cantidades de objetos cuando tienen significado para él y la interacción social con compañeros y maestra, también animan al niño a intercambiar ideas con sus compañeros. Los estudiantes al establecer relaciones y comparaciones de todo tipo, ya sean entre objetos, formas, figuras, tendrán la posibilidad de fortalecer y desarrollar su pensamiento lógicomatemático (Kamii, 2003).

CONCLUSIONES

En este trabajo se identificó, que, para favorecer el desarrollo de la noción de número y del conocimiento lógico matemático del niño, se emplean tres principios de enseñanza: la creación de todo tipo de relaciones, donde se anima al niño a estar atento y a establecer todo tipo de asociaciones entre las diferentes clases de objetos, acontecimientos y acciones; la cuantificación de objetos, donde se anima al niño a pensar sobre los números y las cantidades de objetos cuando tienen significado para él; la interacción social con compañeros y maestros, donde se anima al niño a intercambiar ideas con sus compañeros. Las negociaciones en situaciones de conflicto son especialmente adecuadas para el desarrollo de nociones matemáticas. Resolver problemas en situaciones que le son familiares y que implican agregar, reunir, quitar, igualar, comparar y repetir, son algunos de los procesos de enseñanza y aprendizaje identificados que contribuyen al desarrollo de la noción de número. Por otro lado, la utilización de software educativo puede ser de gran ayuda en el aprendizaje de las matemáticas, debido a que las actividades representaban un reto para los niños, brindándoles la posibilidad de reforzar y consolidar habilidades de conteo, mediante la utilización de sonidos, movimientos, figuras, haciendo que los estudiantes se sientan motivados. Los principios de enseñanza para el desarrollo de la noción de número en preescolar permite trabajar la significancia compartida para el uso de la matemática culturalmente situada. Con esta estrategia, la prioridad consiste en rescatar los conocimientos matemáticos de los niños, identificando sus usos en escenarios de lo cotidiano donde se rescata el conocimiento de ellos, y se reafirma el de los otros niños.

ReferencIAs

Bartolini, M. (1998). Verbal interaction in the mathematics classrom: A Vygotskian análisis. In

H. Steinbring, M. G. Bartolini, and A. Sierpinska (Eds.), Languaje and communication in the mathematics classromm. (pp. 65-84). Reston: NCTM.

Candela, A. (1999). Ciencia en el aula. Los alumnos entre la argumentación y el consenso. México: Paidós. 34-44 Pp.

Cantoral, R. (2016). Teoría Socioepistemológica de la Matemática Educativa. Estudios sobre construcción social del conocimiento. México: Gedisa. 379 Pp.

Cantoral, R. (2019). Socio-Epistemology in Mathematics Education. In S. Lerman (Ed.). Encyclopedia of Mathematics Education. Springer Nature: Hidelberg, Germany. 356 Pp.

Cantoral, R., Reyes-Gasperini, D. y Montiel, G. (2014). Socioepistemología, Matemáticas y Realidad. Revista Latinoamericana de Etnomatemática. 7(3): 91-116.

Cardoso, E. y Cerecedo, M. (2008). El desarrollo de las competencias matemáticas en la primera infancia. Revista Iberoamericana de Educación. 47(5): 1-11.

Duek, C. (2010). Infancia, desarrollo y conocimiento: los niños y niñas y su socialización. Revista Latinoamericana de Ciencias Sociales, niñez y juventud. 8(2): 799-808.

Fernández, A., Molina-Correa, V. y Oliveras, M. (2016). Estudio de una propuesta lúdica para la educación científica y matemática globalizada en infantil. Revista Eureka sobre Enseñanza y Divulgación de las Ciencias. 13(2): 373-383.

Fernández, I., Riveros, V. y Montiel, G. (2017). Software educativo y las funciones matemáticas. Una estrategia de apropiación. Omnia. 23(1): 9-19.

Fuenlabrada, I. (2005). ¿Cómo desarrollar el pensamiento matemático en los niños de preescolar? La importancia de la presentación de una actividad. Curso de Formación y Actualización Profesional para el Personal Docente de Educación Preescolar. México. SEP-Subsecretaría de Educación Básica, Dirección General de Desarrollo Curricular. 1: 279-296.

Fuenlabrada, I. (2009). ¿Hasta el 100? ¡No! ¿Y las cuentas? Tampoco. Entonces ¿Qué? México: SEP. 65 Pp.

Hernández, R., Fernández, C. y Baptista, M. P. (2014). Metodología de la investigación (6ta ed.).

México: Editorial McGraw Hill Education. 613 Pp.

Hernández, J. y Pérez, G. (2018). Estrategias para favorecer la habilidad del conteo en niños de nivel Preescolar. Perspectivas Docentes. 28(64).

Kamii, C. (2003). El número en la educación preescolar. Madrid: A. Machado Libros. 32 Pp.

Lezcano, M., Benítez, L. y Cuevas, A. (2017). Usando TIC para enseñar Matemática en preescolar: El Circo Matemático. Revista Cubana de Ciencias Informáticas. 11(1): 168-181.

Pérez, J. (2014). Empleo del software educativo y su eficiencia en el rendimiento académico del cálculo integral en la Universidad Peruana Unión, filial Tarapoto. Apuntes Universitarios. Revista de Investigación. 4(1): 43-56.

Piaget, J. (1973). La representación del niño en el mundo. Madrid: Morata. 101 Pp.

Reséndiz, E. (2004). La variación en las explicaciones de los profesores en situación escolar. Tesis de doctorado, Cinvestav, México. [En línea]. Disponible en: http://funes.uniandes.edu.co/5620/1/ResendizLavariacionAlme2006.pdf. Fecha de consulta: 13 de agosto de 2018.

Reséndiz, E., Correa, S., Medina, K., Nava, C. y Llanos, R. (2014). La enseñanza aprendizaje del número en preescolar y el uso de las TIC. En P. Lestón, (Ed.), Acta Latinoamericana de Matemática Educativa (pp. 2159-2167). México, DF: Comité Latinoamericano de Matemática Educativa.

Reyes-Gasperini, D. y Cantoral, R. (2019). ¿Cómo evaluar la construcción social del conocimiento matemático? Investigación e Innovación en Matemática Educativa. 4(1): 217-225.

Reyes, C. y Garza, A. (2019). ¡Juego, valoro y aprendo en preescolar 2! Situaciones didácticas. México: Trazo Impresión. 8-9 Pp.

Rodríguez, O. y Norato, A. (2004). Imagen para conocer números (Ilustración). [En línea]. Disponible en: http://www.gateandoconelraton.com/inicio/. Fecha de consulta: 13 de agosto de 2018.

SEP, Secretaría de Educación Pública (2013a). Programa de estudio 2011. Guía para la Educadora. Educación Básica. Preescolar. México. [En línea]. Disponible en: http://www.siteal.iipe.unesco.org/sites/default/files/mex_-_educacion_preescolar_.pdf. Fecha de consulta: 13 de agosto de 2018.

SEP, Secretaría de Educación Pública (2013b). Programa sectorial de educación 2013-2018. México. [En línea]. Disponible en: http://www.sep.gob.mx/work/models/sep1/Resource/4479/4/images/PROGRAMA_SECTORIAL_DE_EDUCACION_2013_2018_WEB.pdf. Fecha de consulta: 13 de agosto de 2018.

Sfard, A. (2002). Learning mathematics as developing a discourse. In R. Speiser and C. Maher (Eds.), Proceedings of conference of PME-NA (pp. 23-44). Columbus: Clearing House for Science, Mathematics, and Environmental Education.

Siegenthaler, R., Casas, A., Mercader-Ruiz, J. and Herrero, M. (2017). Habilidades matemáticas iniciales y dificultades matemáticas persistentes. International Journal of Developmental and Educational Psychology. 3(1): 233-241.

Sierpinska, A. (1994). Understanding in mathematics. Studies in mathematics education. Londres: The Falmer Press: 59-84 Pp.

Vergnaud, G. (2010). El niño, las matemáticas y la realidad: Problemas de la enseñanza de las matemáticas en la escuela primaria. México: Trillas. 111 Pp.

Vygotsky, L. (1984). Aprendizaje y desarrollo intelectual en edad escolar. Revista de infancia y

Aprendizaje. 27(28): 70-92.

Vygotsky, L. (2000). Pensamiento y habla. Buenos Aires: Colihue. 191-208. Pp.