Efecto del patrón de
flujo sobre las pérdidas de presión para flujo bifásico a través de lechos
porosos bajo perspectiva fractal
Flow
pattern effect on the pressure drop of biphasic flow through porous media from
a fractal dimension perspective
Edgardo Jonathan
Suárez-Domínguez1*,
Arturo Palacio-Pérez2, Josué
Francisco Pérez-Sánchez1,3, Elena
Izquierdo-Kulich4
*Correspondencia:
edgardo.suarez@uat.edu.mx/Fecha de recepción: 31 de mayo de 2019/Fecha de aceptación: 4 de octubre de 2019/Fecha de publicación: 31 de enero
de 2020.
1Universidad
Autónoma de Tamaulipas, Facultad de Arquitectura, Diseño y Urbanismo, Centro
Universitario sur, Circuito Universitario s/n, Tampico, Tamaulipas, México, C.
P. 89000. 2Universidad Nacional Autónoma de México, Instituto de
Ingeniería, Coyoacán, Ciudad de México, México. 3Tecnológico
Nacional de México, Instituto Tecnológico de Ciudad Madero, Centro de
Investigación en Petroquímica, Altamira, Tamaulipas, México. 4Universidad
de la Habana, Facultad de Química, Departamento de Química-Física, Vedado, La
Habana, Cuba.
Resumen
La
descripción del comportamiento de un flujo bifásico, a través de lechos
porosos, por medio de modelos, basados en las
ecuaciones de fenómenos de transporte,
se dificulta debido a la irregularidad geométrica de los canales que se
forman entre las partículas sólidas que constituyen el lecho. Los modelos
deterministas desarrollados para flujos monofásicos requieren del ajuste de
constantes empíricas y no pueden extrapolarse a flujos bifásicos, donde el
patrón de flujo generado en el sistema influye significativamente sobre el
comportamiento del flujo total y las pérdidas
de presión por fricción. Por lo anterior, en este trabajo se presenta un
modelo para describir el comportamiento del
flujo bifásico en función del patrón de flujo y de la morfología, las
dimensiones y las condiciones de operación del lecho poroso, cuya obtención se basó en un formalismo, empleando conjuntamente las ecuaciones de
conservación de la cantidad de movimiento, la geometría fractal y el cálculo diferencial fraccional. El modelo predice que,
para una misma composición del flujo bifásico, el patrón de flujo influye
significativamente sobre las pérdidas de presión por fricción, habiendo un
incremento cuando una de las fases se encuentra dispersa en el seno de la otra.
Por otro lado, el incremento de la dimensión
fractal de los poros causa a su vez un
incremento de las pérdidas de presión por fricción. El modelo presenta
limitaciones asociadas a las consideraciones establecidas durante su obtención,
de tal manera que sólo es válido cuando los efectos de la tensión superficial
son más significativos que los gravitatorios, despreciándose los efectos de
esos últimos sobre el patrón de flujo, así como para el estado estacionario.
Palabras clave: reservorio fractal, lecho poroso, flujo complejo,
ecuación fraccional de transporte,
predicción de caída
de presión.
Abstract
The description of the behavior of a biphasic flow through porous beds
by means of models based on the equations of transport phenomena is made
difficult due to the geometric irregularity of the channels that are formed
between the solid particles that make up the bed. Deterministic models developed for single-phase flows require the
adjustment of empirical constants and cannot be extrapolated to biphasic flows,
where the flow pattern generated in the system significantly influences the behavior of the total flow and the frictional pressure
losses. Therefore, in this paper, we present a model to describe the behavior
of the biphasic flow in relation to the flow
pattern and the morphology, dimensions, and operating conditions of the
porous bed, whose obtainment was based on a hierarchy
that used the equations for
conservation of momentum, fractal geometry and fractional differential calculus
jointly. The model predicts that, for the same composition of the biphasic
flow, the flow pattern significantly influences friction pressure losses, with
an increase when one of the phases is
dispersed within the other. On the other hand, the increase in the
fractal dimension of the pores, in turn, causes an increase in pressure loss
due to friction. The model has limitations associated with the considerations
established during its collection, since it is only valid when the effects of
surface tension are more significant than the gravitational effects, the
effects of the latter being disregarded on the
flow pattern, as well as for the stationary state.
Keywords: fractal reservoir, porous
bed, complex flow, fractional equation of transport, pressure drop prediction.
Introducción
El flujo a
través de lechos porosos es un proceso que se asocia con diferentes operaciones
unitarias que se llevan a cabo en la industria
(Pesavento y col., 2017), tales como los procesos
continuos de adsorción (Flury y Aramrak,
2017), reacciones químicas heterogéneas o
catalizadas por sólidos (Ledesma-Durán y col., 2017), filtración e intercambio iónico, entre otras (Bear, 2018). Este
fenómeno se puede observar en la naturaleza, asociado al movimiento de las aguas subterráneas, y en los
procesos de extracción de petróleo crudo desde yacimientos porosos (Kokubun y col., 2018). En dicho contexto, los estudios con
soluciones analíticas que se han llevado a cabo, para describir y modelar el
comportamiento de estos procesos, asumen que
el flujo es monofásico. Sin embargo, pueden presentarse situaciones en
las cuales se genera un flujo bifásico, como cuando se extraen crudos pesados
con agua en su composición, o se emplean productos químicos para disminuir la
viscosidad e incrementar la eficiencia de la explotación de
los yacimientos.
La
presencia de las partículas en el lecho causa una pérdida de presión
significativa, debido a la tensión de corte en la pared de estas, de aquí que
los valores de flujo monofásico que se puedan lograr para una fuerza directora
aplicada son mucho menores que los que se logran en un tubo (Hjelmeland y Larrondo, 1986). El área superficial del
sólido que se encuentra en contacto con el fluido depende de forma compleja de
la morfología de las partículas, de la distribución de tamaños, de la
disposición espacial entre las mismas, y de la porosidad del lecho (Valdes-Perez y col., 2012). Estos factores se consideran
habitualmente a través del ajuste de
parámetros empíricos de los modelos que se emplean para predecir el
comportamiento del flujo (Mahzari y col., 2018). Debido a la tensión de corte, es de esperar
que el incremento en el área superficial por unidad de volumen del sólido,
conlleve a un incremento de las pérdidas de
presión por fricción, de ahí la
importancia de disponer de modelos
fenomenológicos que permitan tomar en cuenta de forma explícita tales
efectos. La descripción es aún más compleja en el caso de flujo bifásico, donde
además de los factores antes mencionados, influyen los patrones de flujo que se
puedan presentar en estos sistemas (Huang y
col., 2018).
El objetivo
de este trabajo consistió en obtener un modelo para predecir el comportamiento
del flujo bifásico y las pérdidas de presión por fricción, que tome en cuenta
de forma explícita el efecto de la morfología del lecho y los patrones de flujo
que se pueden presentar.
MATERIALES Y MÉTODOS
Consideraciones
establecidas para la obtención del
modelo
Para la
obtención del modelo se establecen las siguientes consideraciones: 1) el área
de flujo se visualiza formada por un conjunto de poros circulares con un
perímetro irregular, los cuales, se caracterizan a través de un valor de radio
promedio R y dimensión fractal f, y que se encuentran delimitados
por las partículas; 2) el régimen de flujo es laminar; 3) estado estacionario
y; 4) se considera que el fluido está compuesto por dos líquidos newtonianos e
incompresibles inmiscibles entre sí, donde en dependencia de los efectos de
tensión superficial y de mezclado entre ambos se pueden generar 2 patrones de flujo
básicos. El primero es una emulsión muy útil en el caso de aplicación de
técnicas EOR (Perazzo y col., 2018), en la cual, uno
de los líquidos se encuentra en forma dispersa en el seno del otro, y el
segundo es un patrón de flujo anular, en el cual, uno de los fluidos presenta
una mayor afinidad por las paredes del sólido, de tal manera que se mueve en
contacto con estas, mientras que el otro fluido se mueve por el centro de los
poros.
La
dimensión fractal de dichos canales se determina mediante una observación de la
morfología del lecho en un tamaño equivalente al radio de las partículas que
forman el lecho, y se calcula mediante una fotografía y el empleo de un
programa de tratamiento de imágenes. En este sentido, aunque todos los canales
son de hecho de formas y tamaños diferentes,
se va a considerar un tamaño promedio R y un valor de dimensión
fractal promedio f, que son parámetros que dependen de numerosos
factores, entre los que se pueden mencionar el tamaño y forma de las partículas,
el empacamiento que se establezca entre estas y la porosidad
del lecho.
Análisis de
la morfología del
lecho
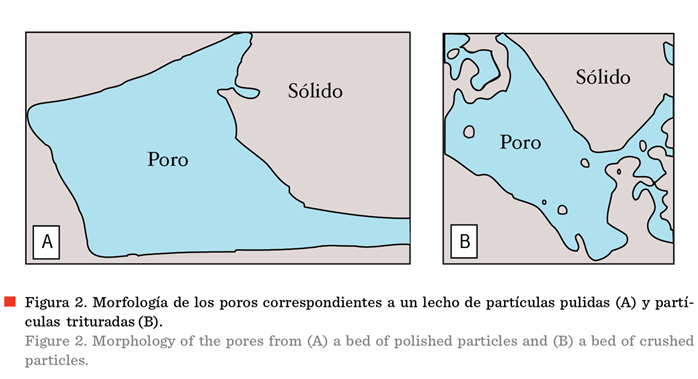
En la Figura 1 se muestran las fotografías de 2 lechos porosos, uno compuesto por sólidos
redondeados por procesos de meteorización (A) y el otro por rocas trituradas
(B). En cada una de estas imágenes se observa
en un recuadro rojo la sección considerada
para la caracterización de la morfología de los poros. En la Figura 2 se
muestran las imágenes correspondientes a los
contornos de los poros, donde los valores de dimensión fractal y porosidad se determinaron mediante
el empleo del programa ImageJ v1.40g, en el cual,
cada imagen a color se convierte en una imagen de 8 bits; a partir de esta, se
obtiene una imagen binaria del patrón, a la que se le determina la dimensión fractal
vertical y horizontal de las imágenes (Rasband, 2018), siendo para las partículas redondas f
= 1.042 4 y para las partículas trituradas
f = 1.125 6.

Debido a
que el perímetro de los poros presenta una morfología irregular, el valor del
área del poro se determina mediante la integral fraccional de orden igual a la
dimensión fractal:
![]() (1)
(1)
Donde:
k (m) es un parámetro relacionado con la
precisión de la medición del tamaño del poro, q es el ángulo determinado en coordenadas
polares para cada punto del círculo irregular que conforma el poro, ![]() es el operador que representa la integral
fraccional, la cual se determina con el radio en coordenadas radiales (r)
a lo largo del tiempo (t), como:
es el operador que representa la integral
fraccional, la cual se determina con el radio en coordenadas radiales (r)
a lo largo del tiempo (t), como:
![]() (2)
(2)
y
es la función gamma dada a través de un parámetro matemático (x):
![]() (3)
(3)
La solución
de la integral fraccionaria (2), trasladándolo
a valores geométricos, es:
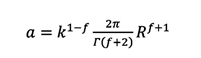 (4)
(4)
Donde:
R representa al radio del poro (m). En
esta descripción de la morfología del poro, el radio R se considera una
variable determinista, mientras que el
perímetro del canal es una variable
aleatoria que se caracteriza a través de la dimensión fractal.
Es importante
señalar que la dimensión fractal (f) tiene un valor diferente
numéricamente al de tortuosidad, utilizado también para caracterizar un medio
poroso, donde una dimensión fractal alta se relaciona con una tortuosidad alta (Valdéz-Cepeda
y Olivares-Sáenz, 1998).
Algunos
autores han correlacionado los diversos valores de tortuosidad, constricción y
porosidad (Berg, 2014). En este trabajo, la dimensión
fractal permite funcionar como la variable dominante, aunque en un futuro
podrían considerarse los elementos en conjunto,
a partir de una modelación con
CFD.
Determinación del
perfil de velocidad y las pérdidas de presión por fricción cuando el patrón de
flujo se corresponde con una emulsión
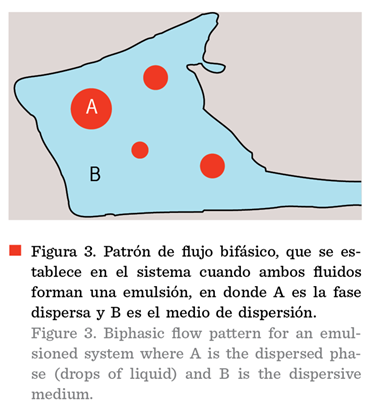
En la
Figura 3, se muestra una representación del patrón de flujo correspondiente al
caso, en el cual se tiene un sistema de fluido bifásico con formación de una
emulsión, donde A corresponde a la fase dispersa (gotas de líquido) y B
corresponde al medio de dispersión.
En el caso
de los flujos en tubos, las emulsiones se visualizan como un flujo en una sola
fase, cuya viscosidad se afecta por la presencia de la fase dispersa
(Suárez-Domínguez y col., 2018). En este caso, la viscosidad de
la emulsión mE (Pa·s) se
puede estimar a través de la
relación:
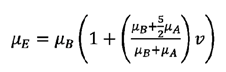 (5)
(5)
Donde:
mA (Pa·s)
es la viscosidad de la fase dispersa, mB (Pa·s)
es la viscosidad del medio de dispersión y v representa la fracción en
volumen de la fase dispersa. En este caso, se utiliza la ecuación 5, que da una expresión para la viscosidad efectiva de una
emulsión que ha sido probada para
crudos del norte de México. Sin embargo, pueden considerarse otro tipo de
ecuaciones (Mendoza y Santamaria-Holek, 2010) en
dependencia del caso analizado.
Para
estimar el flujo que pasa a través de un canal irregular, se parte de la
estimación del comportamiento de la velocidad con respecto a la distancia r
desde el centro del canal, para lo cual, se parte de la ecuación de cantidad de
movimiento para el sistema de coordenadas
cilíndricas, donde, a partir de las
consideraciones establecidas, se obtiene
la ecuación diferencial
parcial:
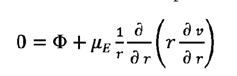 (6)
(6)
Donde:
F (Pa/m) es el gradiente de presión,
sujeta a las condiciones de
contorno:
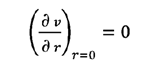 (7a)
(7a)
![]() (7b)
(7b)
La solución
analítica exacta de esta ecuación está
dada por:
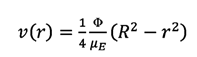 (8)
(8)
Donde:
La
distancia R desde el centro hasta la pared del canal varía
aleatoriamente, debido a la morfología irregular del área de flujo del canal.
Por esta razón, para obtener el valor del flujo q (m3/s) se
integra la velocidad con respecto al área de flujo, para lo cual se toma en
cuenta el carácter irregular de esta área, aplicando una integral fraccional de
orden f:
![]() (9)
(9)
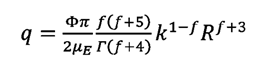 (10)
(10)
Donde:
f es la dimensión fractal del perímetro del canal y cuantifica el carácter irregular y
aleatorio de la distancia r, y que puede considerarse como una buena
aproximación del medio. El flujo total Q (m3/s) se estima
como el producto del flujo q y el número de canales de flujo n,
el cual se determina como el área disponible para el flujo dividido por el área
de un canal:
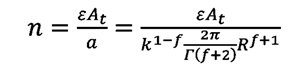 (11)
(11)
Donde:
e es la porosidad del lecho, de tal manera que:
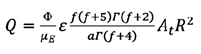 (12)
(12)
y definiendo la velocidad V0
como la relación entre el flujo total y el área total del lecho se
obtiene:
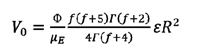 (13)
(13)
El valor de
R depende de la porosidad del lecho y del tamaño de partículas. Para
estimar el valor de R, las ecuaciones (5) y (13) se expresan en función de las variables no dimensionales:
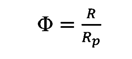 (14a)
(14a)
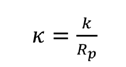 (14b)
(14b)
Donde:
Rp (m) es el radio promedio de las partículas, de tal
manera que el área promedio a del canal de flujo y la velocidad V0
se estiman a través
de las relaciones:
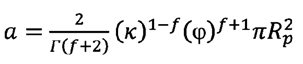 (15)
(15)
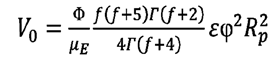 (16)
(16)
Tomando en
cuenta de que existe una relación entre el
área de los poros y el área ocupada por las partículas observada en las
escalas macroscópica y microscópica se asume:
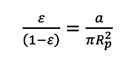 (17)
(17)
Donde:
El término
de la izquierda de la ecuación (17) representa la relación macroscópica entre
el área disponible para el flujo y el área
ocupada por las partículas, mientras que en el lado derecho se presenta
la relación microscópica entre el área estimada del canal de flujo y el área
por una partícula. A partir de las ecuaciones
(15) y (17)
se obtiene:
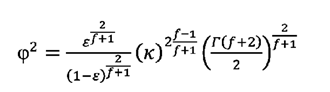 (18)
(18)
Sustituyendo la ecuación (18) en la ecuación (16) se
obtiene:
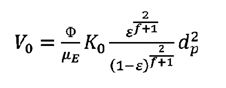 (19)
(19)
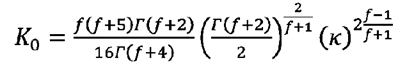 (20)
(20)
Donde:
dp (m) representa el diámetro promedio de las partículas y el valor de la precisión k,
que debido a la escala posible de
medición (Mandelbrot,
1989) se selecciona
de tal manera
que:
![]() (21)
(21)
A partir de
la ecuación (19) se despeja el gradiente de presión:
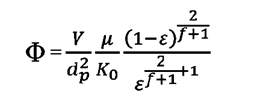 (22)
(22)
Debido a la
morfología irregular de los canales de flujo, hay que considerar que la
distancia longitudinal recorrida por el flujo es mayor que la distancia de la
línea recta que une a los puntos de entrada y de salida del sistema, de tal
forma que, el gradiente de presión se representa a través de la derivada
fraccional de la longitud del lecho, lo que permite obtener la ecuación
diferencial fraccional:
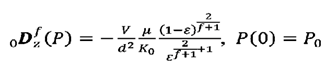 (23)
(23)
cuya
solución está dada
por:
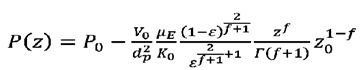 (24)
(24)
Donde:
z0 representa la precisión en la medición
de la longitud del lecho. A partir de la relación
anterior se obtiene que las pérdidas de presión por fricción DP (Pa), para un lecho poroso de longitud L, pueden estimarse
a través de la relación:
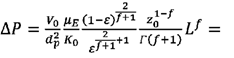
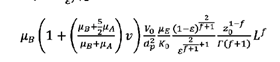 (25)
(25)
donde debe cumplirse que:
![]() (26)
(26)
La ecuación
(25) permite estimar el comportamiento de las pérdidas de presión por fricción,
para flujo bifásico en lecho poroso, cuando los líquidos se disponen entre sí
formando una emulsión.
Determinación del
perfil de velocidad y las pérdidas de presión por fricción, cuando el patrón de
flujo se corresponde con un flujo bifásico
anular
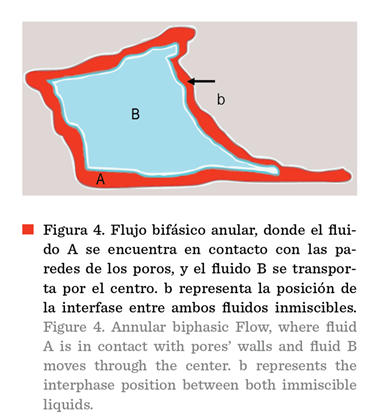
En la
Figura 4 se muestra el patrón de flujo correspondiente al caso, en el cual, se
tiene un sistema bifásico, donde el fluido A se encuentra en contacto con las
paredes de los poros, y el fluido B se mueve por el centro,
de tal manera que, se establece un patrón
de flujo anular. Este caso se propone como similar al correspondiente, cuando
existe una mayor afinidad del agua con el sólido y este se encuentra adsorbida
en él.
Para
determinar el perfil de velocidad que se establece en el sistema, se parte de
la ecuación de cantidad de movimiento, tomando en cuenta las condiciones establecidas, de tal manera que, se obtiene el sistema de ecuaciones diferenciales:
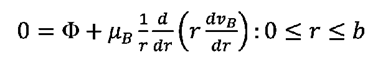 (27a)
(27a)
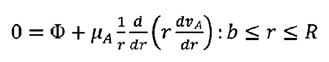 (27b)
(27b)
sujeto a
las condiciones frontera:
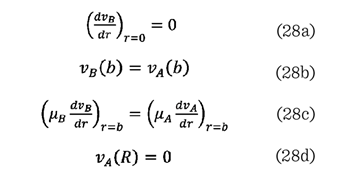
y
cuya solución exacta
está dada por:
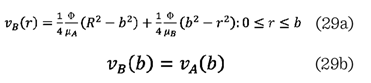
El valor
del flujo total se obtiene a través de la integral fraccional con respecto al
área de flujo, tomando en cuenta la
morfología fractal del poro, por lo que es necesario el empleo de la integración
de orden fraccional. En este caso, se tiene
para el fluido B, que se mueve
por el centro
del poro:
![]()
![]() (30)
(30)
Donde:
a representa la posición no dimensional de la interfase y l cuantifica la relación entre las viscosidades
de ambos fluidos:

mientras que para el fluido que se encuentra en contacto
con la pared:
(32)
![]()
![]()
![]()
de tal forma que, el flujo total que pasa a
través de un canal está dado por la suma de ambos fluidos y se escribe de la
forma siguiente:
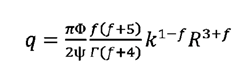 (33)
(33)
El
parámetro y (Pa·s) representa la viscosidad global del sistema (Tan y
col., 2015), y su valor depende de las viscosidades y disposición de cada uno
de los fluidos con respecto a la pared del poro, de la morfología de este, caracterizada a través de la dimensión fractal
y de la posición no dimensional de la interfase, y se determina de acuerdo con la relación:
(34)
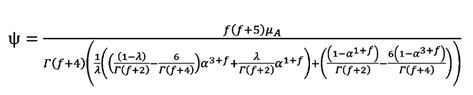
La posición
no dimensional de la interfase se encuentra
estrechamente relacionada con la composición del sistema, y si esta se expresa
en base a la fracción en volumen del fluido que se mueve por el centro del poro
se obtiene:
(35)
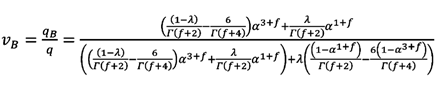
La ecuación (33) es análoga a la ecuación (10), por lo que siguiendo las mismas deducciones que llevan de la ecuación (10) a la ecuación
(25), se obtiene la expresión para predecir las pérdidas de presión por fricción en
este sistema:
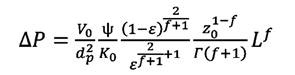 (36)
(36)
RESULTADOS Y DISCUSIÓN
Predicciones teóricas
Los
patrones de flujo bifásico que se generan, para el caso de flujo laminar en
tubos, dependen de la diferencia de densidad entre los líquidos y la tensión interfacial, entre otros factores (Kleinstreuer,
2017; Wopara e Iyuke,
2018); y se encuentran además estrechamente relacionados con la forma en que se
realiza el inyecto de un fluido en el seno
del otro. De esta manera, se pueden
disminuir significativamente las
pérdidas de presión por fricción
asociadas al transporte de un fluido
de alta viscosidad, inyectando otro de menor viscosidad y densidad semejante en
la pared del tubo (Suárez-Domínguez, 2017), lo cual se puede lograr
mediante un dispositivo de inyección apropiado.
La
situación es mucho más compleja en el caso de los lechos porosos, debido a la
cantidad y aleatoriedad de los canales de flujo que se establecen, los cuales
tienen un radio significativamente pequeño (Basu y
col., 2019). Dentro de cada canal del lecho poroso, es prácticamente imposible
generar un patrón de flujo determinado mediante un dispositivo de inyección,
como en el caso de los tubos, aunque la adición de un agente emulsionante o desemulsionante puede facilitar que se transporte una
emulsión o se genere un flujo bifásico anular, respectivamente. Por otra parte,
debido al pequeño radio de los canales de flujo, los efectos de tensión interfacial, en la interfase y en
la superficie del sólido, son mucho más importantes que en el caso del flujo en
tubos, e influyen en la generación del patrón de flujo que se forme en el
sistema, de ahí la importancia del uso de agentes tensoactivos
en estos sistemas (Kamal, 2016). Desde el punto de vista práctico, lo
importante es determinar, para un sistema
bifásico específico, cuál de los
patrones de flujo favorece la disminución
de las pérdidas de presión por fricción, y actuar en consecuencia (Wang
y col., 2019).
Para obtener las predicciones teóricas se consideraron dos líquidos inmiscibles
entre sí, el líquido 1 con viscosidad de 5 Pa·s y el
líquido 2 con viscosidad de 0.1 Pa·s, donde el líquido menos viscoso se encuentra
en menor proporción, y puede
presentarse en forma de fase dispersa en el seno del fluido menos viscoso,
formando una emulsión, y puede estar como fase completamente separada o puede
existir una separación parcial de las fases, en la cual, parte del fluido 1 se
encuentra como fase dispersa, y la otra parte como fase separada. Se consideró
un medio poroso hipotético, con las
dimensiones y condiciones de operación: dp = 0.01 m, e = 0.4,
L = 100 m y V0 = 10-4 m/s-1.
Se
encontraron diferentes comportamientos al analizar teóricamente como varía la
caída de presión por fricción DP (Pa), con respecto a la
fracción en volumen del fluido menos viscoso, considerando como parámetro la
dimensión fractal de los poros, sin considerar la forma de la figura geométrica de las rocas, ni el tipo de superficie
que presentan (lisa o rugosa), para los siguientes casos: Caso A:
el flujo menos viscoso se presenta como una fase dispersa en el seno del fluido
menos viscoso de poro; Caso B: separación total de las fases, en la
cual, el fluido menos viscoso se transporta por el centro del poro; Caso C:
separación total de las fases, donde el fluido menos viscoso se transporta en
contacto con la pared; Caso D: se considera que una fracción del flujo
menos viscoso se transporta en contacto con la pared del tubo, mientras que la
otra parte se encuentra como fase dispersa (separación parcial de las fases).
En este sentido, el parámetro de control, para generar cada uno de estos casos,
es el patrón de flujo bifásico que se supondrá, derivado de la observación de
los casos presentados en campo.
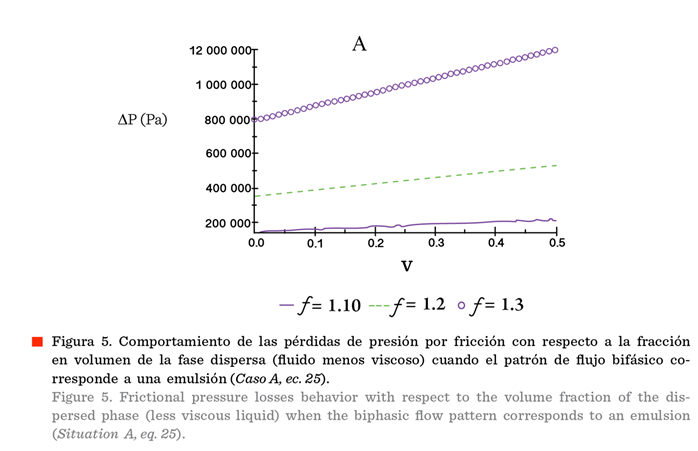
En la
Figura 5, se muestra el comportamiento de las pérdidas de presión por fricción,
con respecto a la fracción en volumen del fluido
menos viscoso, el cual se presenta en forma de fase dispersa en el seno del
fluido más viscoso (Caso A).
Contrariamente a lo que suele ocurrir durante la mezcla de líquidos miscibles,
donde la viscosidad de la mezcla disminuye con la fracción en volumen del
líquido menos viscoso, la viscosidad de una emulsión se incrementa con la
fracción en volumen de la fase dispersa, lo que se manifiesta en el incremento
de las pérdidas de presión por fricción para una velocidad de flujo requerida.
Esto se explica debido a que las gotas dispersas distorsionan el patrón de flujo del medio de dispersión (Ismail y col., 2015), de tal manera que se incrementa la
disipación de la energía producto del rozamiento entre las capas de flujo.
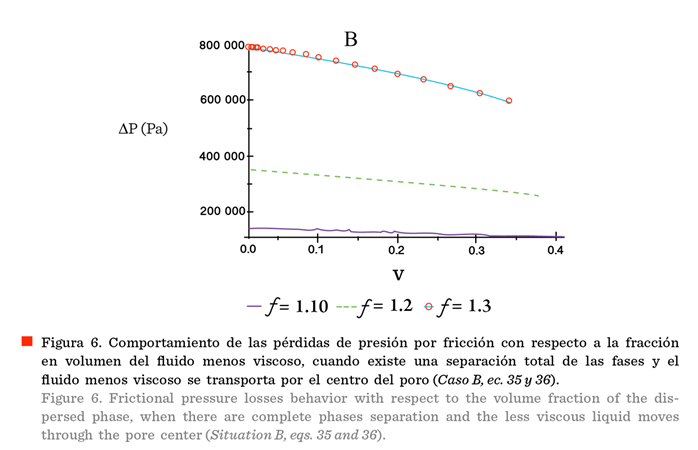
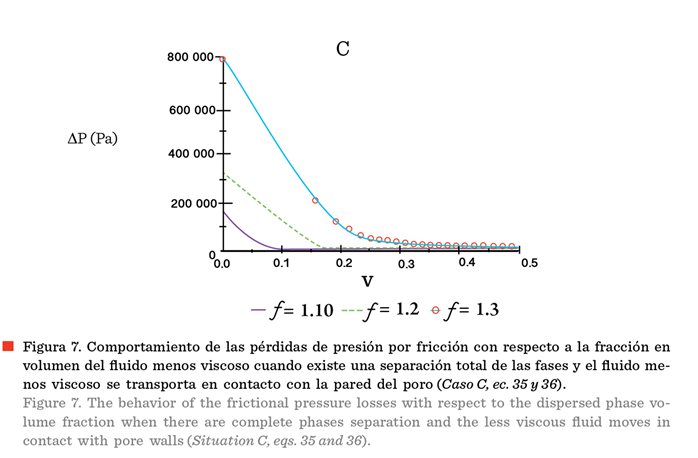
En las
Figuras 6 y 7, se muestran los comportamientos predichos para el caso en que se
establezca un flujo bifásico anular, en el cual existe una separación total de
las fases, donde se ha considerado que el fluido menos viscoso se transporta
por el centro de los poros (Figura 6, Caso B) y en contacto con la pared del poro (Figura 7, Caso
C). En ambos casos, las pérdidas de presión por fricción disminuyen con el
incremento de la fracción en volumen del fluido
menos viscoso, y esta disminución es mucho
más significativa cuando el fluido se transporta
en contacto con la pared del poro. Dichos resultados son esperados si se
toma en cuenta que las pérdidas de presión por fricción son directamente
proporcionales a la tensión de corte en la pared del poro (Hassanean
y col., 2016; Mucharam y col., 2017), la cual, a su
vez, es directamente proporcional a la viscosidad del fluido que se encuentra en
contacto con esta.
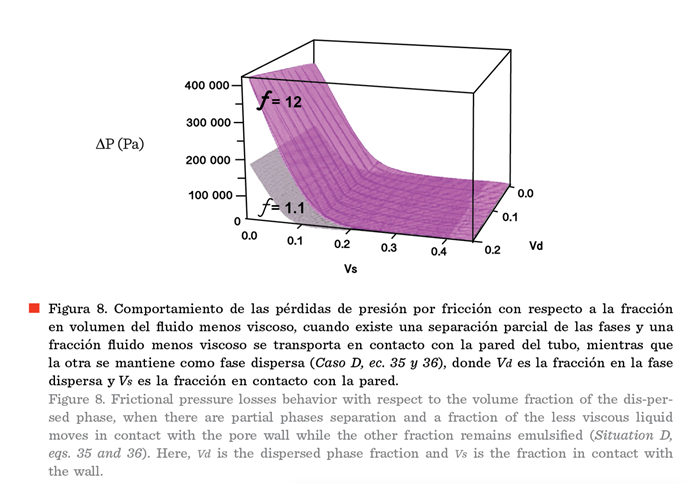
En la
Figura 8 se aprecia un gráfico en 3
dimensiones, donde las superficies mostradas representan la variación de
las pérdidas de presión por fricción con respecto a la fracción del fluido
menos viscoso que se encuentra en forma dispersa (Vd), y la fracción que se encuentra
en contacto con la pared del tubo (Vs), por lo que se corresponde con un patrón combinado
de flujo bifásico anular, donde el fluido que se transporta por el centro es una emulsión (Caso D). Esta
situación se corresponde con una separación
parcial de las fases, similar a lo observado por Piroozian
y col. (2017).
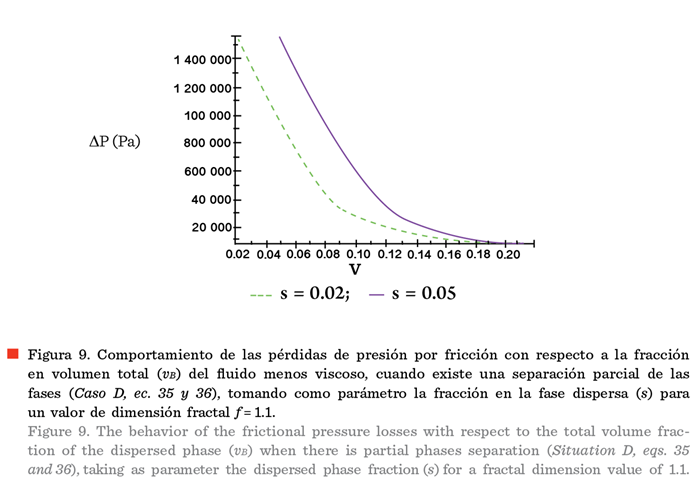
Como
también se aprecia en la Figura 9, que representa el comportamiento de las
pérdidas de presión por fricción, con respecto a la fracción en volumen total
del fluido menos viscoso, considerando como parámetro la fracción de este, que se encuentra presente en la fase
dispersa, se predice que las pérdidas de presión por fricción se incrementan
con la fracción en volumen de la fase dispersa, y la disminución de la fracción del fluido menos viscoso, que se ha separado de
la emulsión y tiende a transportarse en contacto con la
pared del tubo.
Con
respecto al efecto de la dimensión fractal del poro, se observa que en todos
los casos las pérdidas de presión por fricción se incrementan con este
parámetro. Esto se debe a que el incremento de la dimensión fractal causa un
incremento en el área superficial de la pared
de los poros (Rahner y col., 2018) a través de
los cuales, se mueve el fluido, lo que incrementa las fuerzas de rozamiento
entre el fluido y las paredes del sólido, con el consiguiente incremento de la
disipación de energía.
El modelo presenta limitaciones que se encuentran asociadas a las consideraciones que fueron
establecidas durante su obtención, de tal
manera que, es válido cuando los efectos de tensión superficial son más
significativos que los gravitatorios, por lo que la acción de estos últimos
sobre el patrón de flujo puede ser despreciada y cuando el flujo se encuentra
en estado estacionario.
CONCLUSIONES
Partiendo
de las ecuaciones de conservación de la
cantidad de movimiento, y aplicando el formalismo de la geometría
fractal y el cálculo diferencial
fraccionario, se presenta un modelo para describir el comportamiento del
flujo bifásico, como función de las dimensiones
y condiciones de operación del lecho poroso, la morfología del mismo y
el patrón de flujo, el cual puede emplearse para predecir el efecto de estos
parámetros sobre las pérdidas de presión por fricción. En este caso, se obtuvo
que, para una misma composición del flujo
bifásico, el patrón de flujo que se genera en el sistema influye de
forma significativa sobre las pérdidas de presión por fricción, las cuales se
incrementan si una de las fases se presenta de
forma dispersa en el seno de la otra. Por otra parte, se predice que el
incremento de las irregularidades de las
partículas, que se manifiesta en el incremento de la dimensión fractal
de los poros, causa a su vez un incremento significativo de las pérdidas de presión
por fricción.
Agradecimientos
Esta
investigación se realizó con apoyo del fondo SENER-CONACYT sector
HIDROCARBUROS, bajo proyecto número 282278. El autor EJSD agradece el apoyo PRODEP como NPTC y PROFEXCE.
ReferencIAs
Basu, M., Zahoor, A., and Khan, R. A. (2019). Review of Fluid Flow and Heat Transfer through
Microchannels. Journal of Scientific and Technical Advancements. 5(1):
17-20.
Bear, J. (2018). Modeling Phenomena of Flow and
Transport in Porous Media. Springer: Cham. 1-98 P p
Berg, C. F. (2014). Permeability description by
characteristic length, tortuosity, constriction and porosity. Transport in
porous media. 103(3): 381-400.
Flury, M. and Aramrak, S. (2017).
Role of air-water interfaces in colloid transport in porous media: A review. Water
Resources Research. 53(7): 5247-5275.
Hassanean, M. H., Awad, M. E.,
Marwan, H., Bhran, A. A., and Kaoud, M.
(2016). Studying the rheological properties and the influence of drag reduction
on a waxy crude oil in pipeline flow. Egyptian Journal of
Petroleum. 25(1): 39-44.
Hjelmeland, O. S. and Larrondo, L. E.
(1986). Experimental investigation of the effects of temperature, pressure, and
crude oil composition on interfacial properties. SPE Reservoir Engineering.
1(04): 321-328.
Huang, S., Yao, Y., Zhang, S., Ji, J., and Ma, R.
(2018). A Fractal Model for Oil Transport in Tight Porous Media. Transport
in Porous Media. 121(3):725-739.
Ismail, A. S. I., Ismail, I., Zoveidavianpoor,
M., Mohsin, R., Piroozian, A., Misnan,
M. S., and Sariman, M. Z. (2015). Review of oil–water
through pipes. Flow Measurement and
Instrumentation. 45:357-374.
Kamal, M. S. (2016). A review of gemini surfactants: potential application in enhanced
oil recovery. Journal of Surfactants and Detergents. 19(2): 223-236.
Kleinstreuer, C. (2017). Two-Phase Flow: Theory and Applications.
CRC EE.UU: Press. 69-99 Pp.
Kokubun, M. A. E., Radu, F. A., Keilegavlen,
E., Kumar, K., and Spildo, K. (2018). Transport of
polymer particles in an oil-water flow in porous media: enhancing oil
recovery. Transport in Porous Media.
126(2): 501-519.
Ledesma-Durán,
A., Hernández, S. I., and Santamaría-Holek, I. (2017). Effect of Surface Diffusion on Adsorption–Desorption
and Catalytic Kinetics in Irregular Pores. II. Macro-Kinetics. The Journal of Physical Chemistry C. 121(27): 14557-14565.
Mahzari, P., Taura, U., and Sohrabi,
M. (2018). An improved methodology for estimation of two-phase relative
permeability functions for heavy oil displacement involving compositional
effects and instability. Computational Geosciences. 22(4): 975-991.
Mandelbrot, B. B. (1989). Multifractal measures,
especially for the geophysicist. In C. H. Scholz and B. B. Mandelbrot (Eds.), Fractals
in geophysics (pp. 5-42). Basel: Birkhäuser.
Mendoza, C. I. and Santamaria-Holek,
I. (2010). Rheology of concentrated emulsions of spherical droplets. Applied Rheology. 20(2): 16-23.
Mucharam, L., Rahmawati, S., and Ramadhani, R. (2017). Drag reducer selection for oil pipelinebased laboratory experiment. Modern Applied
Science. 12(1): 112.
Perazzo, A., Tomaiuolo, G., Preziosi, V., and Guido, S. (2018). Emulsions in porous
media: From single droplet behavior to applications for oil recovery. Advances in colloid and interface science. 256:
305-325.
Pesavento, F., Schrefler, B. A., and Sciumè, G. (2017). Multiphase flow in deforming porous
media: A review. Archives of Computational Methods in Engineering.
24(2): 423-448.
Piroozian, A., Hemmati, M., Ismail,
I., Manan, M. A., Rashidi, M. M., and Mohsin, R. (2017). An experimental study
of flow patterns pertinent to waxy crude oil-water two-phase flows. Chemical
Engineering Science. 164: 313-332.
Rahner, M. S., Halisch, M.,
Fernandes, C. P., Weller, A., and dos-Santos, V. S. S. (2018). Fractal
dimensions of pore spaces in unconventional reservoir rocks using X-ray nano-and micro-computed tomography. Journal of Natural
Gas Science and Engineering. 55: 298-311.
Rasband, W. S. (2018). ImageJ, U. S. National Institutes of Health, Bethesda, Maryland, USA. [En
línea]. Disponible en: https://imagej.nih.gov/ij/,1997-2018. Fecha
de consulta: 2 de julio
de 2019.
Suárez-Domínguez,
E. J. (2017). Estudio del transporte estratificado de un líquido de alta
viscosidad y otro de baja viscosidad, Tesis doctoral, Universidad Nacional
Autónoma de México. [En línea]. Disponible en: http://132.248.52.100:8080/xmlui/handle/132.248.52.100/14368.
Fecha de consulta: 26 de septiembre de 2019.
Suárez-Domínguez,
E. J., Pérez-Sánchez, J. F., Palacio-Pérez, A., and Izquierdo-Kulich, E. (2018). New mixing rule for analysis of the influence of a formulation on an extraheavy oil crude viscosity. Revista
Mexicana de Ingeniería Química. 17(1):99-106.
Tan, X. H., Li, X. P., Zhang, L. H., Liu, J. Y., and Cai, J. (2015). Analysis of
transient flow and starting pressure gradient of power-law fluid in fractal
porous media. International Journal of Modern Physics C. 26(04):
1550045.
Valdes-Perez, A., Pulido, H.,
Cinco-Ley, H., and Galicia-Muñoz, G. (2012). Discretization of the resistivity, capillary pressure and relative
permeability for naturally fractured
reservoirs. In Proceedings:
Thirty-Seventh Workshop on Geothermal Reservoir Engineering. [En línea]. Disponible en:
https://pangea.stanford.edu/ERE/pdf/IGAstandard/SGW/2012/Valdesperez1.pdf.
Fecha de consulta: 25 de julio de
2019.
Valdéz-Cepeda, R. D. and Olivares-Sáenz,
E. (1998). Geometría fractal
en la ciencia del suelo. Terra Latinoamericana. 16(3): 277-288.
Wang, W., Fan, D., Sheng, G., Chen, Z., and Su, Y.
(2019). A review of analytical and semi-analytical fluid flow models for
ultra-tight hydrocarbon reservoirs. Fuel. 256: 115737.
Wopara, O. F. and Iyuke, S. E.
(2018). Review of studies on pore-network modeling of wettability effects on
waterflood oil recovery. Journal of Petroleum and Gas Engineering. 9(2): 11-22.